High Standards

The other day I found a post in an online relationship forum that got me thinking. The author of the post had stumbled across a text conversation between his fiancee and one of her girlfriends he wasn’t meant to see in which she belittled his sexual performance and talked up her ex. The author of the post was reasonably distressed, but more than feeling disrespected, he insisted that it was extremely important to him to know that he was the best lover she’d ever had.

Now personally, I don’t think that’s a fair standard, and I started thinking about how I could construct a statistical argument to demonstrate this.

Formalizing the question

Someone has had m sexual partners. Assume it is possible to attribute some kind of rating to each partners sexual ability, such that we can rank partners relative to this rating and clearly identify the best sexual partner thus far observed. If things don’t work out, what is the expected number of new partners needed to be …observed before the previous “high score” is met or surpassed?

We can easily generalize this problem further by restating it mathematically.

WARNING: Mathematical notation ahead! Anything you don’t understand, just skip. I really am just being as precise as possible. Even if my notation is confusing or unfamiliar to you, the strategy and results should still make sense, even if you don’t have a background in probability.

Let $X \sim f (x; θ)$ with pdf $F (x; θ)$
Consider an i.i.d. sample of size $n$ drawn from $X$ , ${X_{1}, X_{2}, \dots X_{n}}$
Let $m = X_{(n)} = max (X_{1}, X_{2}, \dots X_{n})$

We are interested in finding the expected wait time until we observe a value greater than the previously observed max, given the number of samples we’ve already observed. Concretely:

Find the quantity $E [j ∣ i]$ such that $p (j ∣ i) = p (X_{i + j} \geq X_{(i)})$

For simplicity, let’s assume that we know the concrete value taken by the max (rather than just which observation takes the max value). I’d assert that this isn’t really the case in the “best sex partner” question, where we really just have a rank ordering of partners and not a score. Anyway, let’s start with this formulation of the problem: we are interested in finding the exected wait time until we observe a value greater than the previously observed max value, given a concrete score associated with each observation.

Find the quantity $E [j ∣ m]$ such that $p (j ∣ m) = p (X_{i + j} \geq X_{(i)} ∣ m = X_{(i)} & X_{i + 1, \dots i + j - 1} < X_{(i)})$

The Geometric Distribution

If think of the event of finding a new max value as a “success”, then we’re trying to model the number of observations, $j$ , until the first success after a series of failures. In other words, we need the geometric distribution, which has pdf:

$d g eo m (j, p) = p (1 - p)^{j - 1}$

where $p$ is the probability of success. This PDF should make a lot of sense intuitively. If $p$ is the success probability, then $1 - p$ is the failure probability. We want to know the probability that after $j$ observations, we’ve had $j - 1$ failures and one success. Assuming successes and failures are independent events, we can calculate the joint probability by taking the products of the probabilities of each indpendent event, giving us the geometric PDF described above.

Since we defined a “success” as achieving a score greater than or equal to the $m$ , we can extract this probability from the right tail of the pdf, i.e. the complement of the CDF: $p = 1 - F (m)$

xv = seq(-4, 4, .01)
yv = dnorm(xv)
m = 1.5
i=which.max(xv==m)
j=length(xv)
yshift=.1*max(yv)
plot(xv, yv, type='l', xlab="", ylab="", axes=0, ylim=c(-yshift, max(yv)), main="Right tail of PDF = p(x>m)")
polygon(x=c(xv[i], xv[i:j], xv[j]), y= c(0, yv[i:j], 0), col="gray")
#abline(v=m, lty=2)
lines(c(m,m), c(-yshift*.5,max(yv)), lty=2)
#text(m+.5, dnorm(m), 'm')
text(m, -yshift, 'm')

Deriving the expectation of the geometric distribution

The expectation of the geometric distribution is $\frac{1}{p}$ . You can look this up on wikipedia or any math/stats textbook, but just for fun I’m going to derive this expectation here. You can just skip the rest of this section if you’re not interested in this derivation.

Let $p (j) = p (1 - p)^{j - 1}$ .

Let $q = 1 - p$ such that $p (j) = (1 - q) q^{j - 1}$

E [j] = i = 1 \sum \infty i (1 - q) q^{i - 1} = i = 1 \sum \infty i (q^{i - 1} - q^{i}) = i = 1 \sum \infty i q^{i - 1} - i = 1 \sum \infty i q^{i} = \frac{1}{q} i = 1 \sum \infty i q^{i} - i = 1 \sum \infty i q^{i} = (\frac{1}{q} - 1) i = 1 \sum \infty i q^{i} = (\frac{1}{q} - 1) (\frac{q}{( 1 - q ) ^{2}}) = \frac{1}{( 1 - q ) ^{2}} - \frac{q}{( 1 - q ) ^{2}} = \frac{1 - q}{( 1 - q ) ^{2}} = \frac{1}{1 - q} = \frac{1}{p}

See? That wasn’t so bad. Like I said, $E [j] = \frac{1}{p}$ .

Back to the problem.

Expected time to next max value

By translating the problem representation into a geometric random variable, we can infer that $p (j ∣ m) = \frac{1}{1 - F ( m )}$ . This should actually make a lot of sense intuitively. Recall the frequentist interpretation of probability:

$P(x) \approx \frac{count(\text{# of events})}{count(\text{# of trials})}$

Let’s imagine that for some collection of $n$ samples with $X_{(n)} = m$ , $F (m) = \frac{1}{t}$ . The frequentist interpretation of probability essentially asserts that our observed max $m$ is a $1$ in $t$ observation, and so it’ll probably take another $t$ observations before we see another observation at least as large.

We’ve come a long way, but we still have the problem that we don’t actually know $m$ , and if we did we don’t really have access to the CDF. We could construct some sort of measure and try to fit a CDF experimentally, but we can get pretty far analytically.

The missing piece to our solution is an estimator for $m$ given the number of samples we’ve observed. But, if you think about it, we don’t really even need this: what we really need, is an estimator for $p$ . For this, we can just fall back on the frequentist interpretation of probability. Empirically, the max observation in a sample of $n$ observations is a $1$ in $n$ observation, so our empirical estimate of seeing a value at least as large (its CDF complement) is therefore just $\frac{1}{n}$ .

This leaves us with the very simple heuristic that $E [j ∣ i] = i$

… except this isn’t entirely accurate, as we’ll learn in a moment.

How much longer must I wait?

Having gotten this far, what then is the progression of the observation number on which we expect to meet new max values? Let’s investigate this experimentally :

Let $i$ denote the total number of observations thus far and $k$ denote the index of the expected next max observation. Then:

First max: $i = 1, k = 2$
Second max: $i = 2, k = 4$
Third max: $i = 4, k = 8$
Fourth max: $i = 8, k = 16 \dots$

This sequence is $a_{i} = 2^{i}$ . In other words, this quantity exhibits exponential growth, which means it grows very, very quickly.

xv=0:5
plot(1+xv, 2^xv, 
     xlab="Expected # new max values observed", 
     ylab="Size of sample", main="Exponential growth of expected index\nof new max given size of current sample")

Back to the original problem: if someone were to constrain their marriage options to people that are the best sex partners they have to that point experienced, then if they’ve slept with 30 people, they’ve only met approximately 6 candidates for marriage-viable relationships.

Like I said: exponential growth is bad.

Simulation

I’ve cheated a bit by assuming that each new max value comes exactly when it’s expected. This is a stochastic problem and I’ve treated it like it’s discrete. Let’s run some simulations to sanity check our results (and also because simulation is fun).

Normality assumption

For the purposes of this problem, I’m going to constrain my attention to the standard normal distribution for the rest of this analysis. This is a pretty big assumption, but I don’t think it’s completely unreasonable relative to the problem. If there were some way to objectively measure sexual performance, I think it wouldn’t be at all surprising if a random sample of people’s measures exhibited normality. I am definitely ignoring the potential effect of variance on the behavior of the max statistic by specifically assuming the standard normal, but maybe I’ll investigate the effect of variance more later.

Building the simulation

To begin with, let’s define a function that, for some generating distribution, will generate random samples sequentially and track the value and arrival of new max values as they occur in the sample.

max_val_sim = function(fx, k=1e4){
  x_max = 0 #fx(1)
  # Preallocate storage
  vals = c(0, rep(NA_real_, k))
  arrival = c(0, rep(NA_integer_, k))
  j=1 # This will index into storage vectors
  X = fx(k)
  for(i in 1:k){
    x_new = X[i] 
    if(x_new>x_max){
      j = j + 1
      x_max = x_new
      vals[j] = x_max
      arrival[j] = i
    }
  }
  list(values=vals[1:j], time=arrival[1:j])
}

Now let’s wrap this function in another function that will run it repeatedly and return the collected results of all the individual simulations. I don’t actually know how many values will be returned by a given simulation, so I’ll have to be a little creative with how I capture the results of each experiment.

max_val_monte_carlo = function(fx=rnorm, # generating distibution
                               reps=2e3, # Number of repeated resample simulations
                               samples=5e4, # Samples drawn during a given simulation
                               est_extreme_per_run = 20 # estimate of number of extreme values hit per simulation. Performance parameter. Can basically be any arbitrary value.
){
  est_total = est_extreme_per_run*reps # for vector pre-allocation
  indices           = rep(NA_integer_, est_total)
  values            = rep(NA_integer_, est_total)
  arrival_time      = rep(NA_integer_, est_total)
  pre_arrival_wait  = rep(NA_integer_, est_total)
  next_arrival_wait = rep(NA_integer_, est_total) # this will end up being 1 shorter than other storage vectors
  j=0 # to index into storage vectors
  for(i in 1:reps){
    sim = max_val_sim(fx, k=samples)
    m = length(sim$time)
    # Calculate pre-arrival wait (time since last max observed)
    sim_paw = c(sim$time[1], sim$time[2:m]-sim$time[1:(m-1)])
    # Calculate wait to next... This is basically the same as above, just shifted. Probably redundant to even store this.
    sim_naw = c(sim_paw[2:m], NA)
    
    while(j+m > length(arrival_time)){
      print("growing storage vectors...")
      indices           = c(indices,          rep(NA_integer_, est_total))
      values            = c(values,           rep(NA_integer_, est_total))
      arrival_time      = c(arrival_time,     rep(NA_integer_, est_total))
      pre_arrival_wait  = c(pre_arrival_wait, rep(NA_integer_, est_total))
      next_arrival_wait = c(                  rep(NA_integer_, est_total))
    }
    
    # Store outcome of simulation iteration
    j=j+1
    j2=j+m-1
    indices[j:j2]            = seq_along(sim$values)
    values[j:j2]             = sim$values
    arrival_time[j:j2]       = sim$time
    pre_arrival_wait[j:j2]   = sim_paw
    next_arrival_wait[j:j2]  = sim_naw
    j=j2
  }
  # Flush NAs
  arrival_time = arrival_time[!is.na(arrival_time)]
  m = length(arrival_time)
  indices           = indices[1:m] 
  values            = values[1:m] 
  pre_arrival_wait  = pre_arrival_wait[1:m]
  next_arrival_wait = next_arrival_wait[1:m]
  
  # Return
  list(values=values, arrival_time=arrival_time, pre_arrival_wait=pre_arrival_wait, next_arrival_wait=next_arrival_wait, index=indices)
}

With all the pieces in place, let’s run the simulation.

set.seed(123)
system.time(test <- max_val_monte_carlo(reps=1e2)) # 100reps->5s, 1e3->50s

Let’s start by looking at $E [j ∣ m]$ . The following plot is colored based on the log(i) to roughly demonstrate the relationship between E[j|i] and $m$ .

plot(test$values, test$next_arrival_wait, 
     col=(1+floor(log10(test$arrival_time))),
     xlab="m",
     ylab="j|m"
     )

That’s pretty tough to read, but the relationship becomes clearer if we instead visualize the log of $j ∣ m$ .

plot(test$values, log(test$next_arrival_wait), 
     col=(1+floor(log10(test$arrival_time))),
     xlab="m",
     ylab="log(j|m)"
     )

The slight curvature the plot exhibits means that it’s actually growing faster than exponentially.

To sanity check $E [j ∣ m] = \frac{1}{1 - F ( m )}$ , let’s plot it against the simulation results.

expected_wait_time = function(x, cdf=pnorm){
  (1-cdf(x))^-1
}
xv = seq(0,4,.001)
#plot(test$values, test$next_arrival_wait)
#lines(xv, expected_wait_time(xv), lty=2, col='blue')
 
plot(test$values, log(test$next_arrival_wait))
lines(xv, log(expected_wait_time(xv)), lty=2, col='blue')

Looks like our estimator fits the data!

Now let’s take a look at the relationship between the expected wait time and the time at which we observed our last max value.

plot(test$arrival_time, test$next_arrival_wait, 
     col=(1+floor(test$values)),
     xlab="i",
     ylab="j|i"
     )

Yikes. This is a bit more readable in log-log space:

plot(log(test$arrival_time), log(test$next_arrival_wait), 
     col=(1+floor(test$values)),
     xlab="log(i)",
     ylab="log(j|i)"
     )

These plots pretty clearly shows that our expected $j$ is much more accurately estimable given some $m$ than given some $i$ , especially as sample size gets large.

Re-evaluating the growth rate

Earlier, I produced an argument for $2^{n}$ as a reasonable heuristic for the growth rate of the expected wait time to the next new max value. Let’s see how this estimate compares to the experimental data.

xv = 1:20
plot(test$index[1:length(test$values)], log(test$arrival_time))
lines(xv, log(2^(xv)), col="blue")
lines(xv, log(2^(xv-1)), col="red")
lines(xv, log(xv*2^(xv)), col="green")

From our simulations, it looks like $2^{n}$ is a reasonably good heuristic for small sample sizes, but the number of samples needed to achieve new max values for large samples seems to grow even faster than this, at least under the normality assumption we used in the simulation.

To improve our estimate, we need to examine the distribution of the max of a given sample. Following the notation defined earlier: $p (x = X_{(n)}) = p (x \geq X_{1}, x \geq X_{2}, \dots x \geq X_{n}) = F (x)^{n}$ . This distribution is closely related to the Gumbel distribution, which is widely used in extreme value theory: http://stats.stackexchange.com/questions/105745/extreme-value-theory-show-normal-to-gumbel

I don’t really have experience with extreme value theory, so I’m going to experiment with $p (x = X_{(n)})$ directly.

Given $X_{(n)}$ has CDF $F (x)^{n}$ , the PDF is given by $\frac{d}{d x} C D F = n F (x)^{n - 1} f (x)$ . Therefore, to find the expectation we evaluate the following interval:

E [x ∣ n] = \int x n F (x)^{n - 1} f (x) d x

Aaaaand we’re already at an impasse. This integral doesn’t just look difficult to evaluate: according to wolfram, if we adopt the normality assumption closed form solutions are only known up to $n = 5$ .

Although an analytic solution isn’t readily available, we can still use numerical methods to approximate this integral at different values of $n$ to estimate this expectation, and then maybe fit a curve to the result to get an approximation to the analytic solution as a function of $n$ . Although it’ll just be an approximation, it may still be very informative of the behavior of this expectation. In particular, I’m interested to see how quickly this grows, since the $2^{n}$ heuristic fails for large $n$ .

Method 1. Lazy monte carlo simulation of mean, using tools we already built

We can leverage the simulations we’ve already performed to get an estimate: for a given observed max we can attribute this value to samples of increasing size up to the appearance of the next new max value.

Method 2. Monte carlo simulation of mean

The method above is a bit biased though because we aren’t actually generating new samples. To really do this right, we need to draw a new sample of size $n$ each time and evaluate the max value for that sample. Otherwise we’re just loading up our data with autocorrelation and bias.

max_sim_given_n = function(n, reps, fx=rnorm, values=FALSE, mu=TRUE, sigma=TRUE){
  replicate(reps, max(fx(n)))
}

Let’s visualize this distribution for a few values of $n$ just to see how it behaves.

plot(0,0, 
     type='n', 
     xlim=c(0,5), 
     ylim=c(0,2), 
     xlab='x',
     ylab='p(x=X_(n))', 
     main="Distribution of max(X_(n))\nfor increasing values of n"
     )
system.time( sapply(1:4,function(x) lines(density(max_sim_given_n(10^x, 5e3)), col=x)) )
legend('topleft', paste("n=10^", 1:4), lty=1, col=1:4  )

Now let’s run simulations over a full range of $n$ values and visualize the simulated expectation and 95% CI. I’m going to use the median instead of the mean as my simulated expectation to simplify my code a bit. It shouldn’t really make much of a difference, but it’s worth mentioning since formally monte carlo simulation generally uses the mean.

#totx=2e3, reps=2e2 -> 85.63 seconds
#totx=1e3, reps=2e2 -> 15.29 seconds
#totx=1e3, resp=1e2 ->  7.8 seconds
#totx=1e2, reps=1e2 ->  0.14 seconds
totx = 1e3 #2e3 
xv = 1:totx
system.time(CI <- sapply(xv, function(x) quantile(max_sim_given_n(x, 2e2), c(.025, .5, .975))))
plot(0,0, type='n', xlab='log(n)', ylab='E[X_(n)]', xlim=c(0,max(log(xv))), ylim=c(0,max(CI)))
lines(log(xv), CI[2,])
lines(log(xv), CI[1,], col='red', lty=2)
lines(log(xv), CI[3,], col='red', lty=2)

Interestingly, the magnitude of the confidence interval appears to converge to around $1.35$ .

plot(xv, CI[3,]-CI[1,], main="Width of 95% CI for different")
(inter_ci = mean(CI[3,floor(.75*totx):totx]-CI[1,floor(.75*totx):totx]))
abline(h = inter_ci, col='blue', lty=2)

If we look at this in log space, it looks like the magnitude of the CI is still a ways from converging, but it does appear to be converging.

plot(log(xv), CI[3,]-CI[1,])

This isn’t surprising and actually corroborates the one thing I know about extreme value theory: as sample size approaches infinity, the distribution of the max of i.i.d. normals approaches the Gumbel distribution. The convergence of the simulated confidence interval is approaching the 95% CI of the standard Gumbel distribution (the distribution of the max of i.i.d. standard normals). I haven’t been playing with the Gumbel distribution more in this experiment because I’m not really interested in the convergence behavior of this statistic: I want to know how it behaves as a function of sample size.

With this estimate (and confidence bounds) on hand, we can now plug this back into our analytic estimate for $E [j ∣ m]$ to get confident bounds on $E [j ∣ i]$ under the normality assumption:

j_est = 1/(1-pnorm(CI))
plot(xv,j_est[2,], type='l',
     xlab="i", 
     ylab='E[j|i]')
 
plot(0,0, 
     type='n', 
     xlim=c(0,max(xv)),
     ylim=c(0,max(j_est)),
     xlab="i", 
     ylab='E[j|i]')
lines(xv, j_est[1,], lty=2, col='red')
lines(xv, j_est[2,])
lines(xv, j_est[3,], lty=2, col='red')

Yikes! The upper bound of the confidence interval is growing a lot faster than than the expected value of the lower bound. This is clearer if we zoom in a bit.

# Upper bound of CI grows rapidly
plot(0,0, 
     type='n', 
     xlim=c(0,max(xv)),
     #xlim=c(0,100), 
     ylim=c(0,max(j_est[,1:100])),
     xlab="i", 
     ylab='j')
lines(xv, j_est[1,], lty=2, col='red')
lines(xv, j_est[2,])
lines(xv, j_est[3,], lty=2, col='red')

If we look at this in log space, we can see that the expectation and both bounds of the CI are stabilizing.

log_j_est = log(1/(1-pnorm(CI)))
plot(0,0, type='n', xlim=c(0,max(xv)), ylim=c(0,max(log_j_est)), xlab="i", ylab='log(j)')
lines(xv, log_j_est[1,], lty=2, col='red')
lines(xv, log_j_est[2,])
lines(xv, log_j_est[3,], lty=2, col='red')

Presumably, this is the simulation converging to the standard Gumbel distribution. but in log-log space it looks like we’re still a ways off from converging.

log_j_est = log(1/(1-pnorm(CI)))
plot(0,0, type='n', xlim=c(0,max(log(xv))), ylim=c(0,max(log_j_est)), xlab="log(i)", ylab='log(j)')
lines(log(xv), log_j_est[1,], lty=2, col='red')
lines(log(xv), log_j_est[2,])
lines(log(xv), log_j_est[3,], lty=2, col='red')

Let’s sanity check how well our results capture the behvaior observed in the original simulation.

# overlay with our original simulation
lim_x = max(log(xv))
log_arr = log(test$arrival_time)
plot(log_arr[log_arr<=lim_x], log(test$next_arrival_wait)[log_arr<=lim_x], 
     #col=(1+floor(test$values)),
     xlab="log(i)",
     ylab="log(j|i)",
     xlim=c(0,lim_x)
     )
lines(log(xv), log_j_est[1,], lty=2, col='red')
lines(log(xv), log_j_est[2,], lty=2, col='blue')
lines(log(xv), log_j_est[3,], lty=2, col='red')

Looks like a pretty good fit, but at first glance it seems to be shifted up a bit. I think this isn’t a reflection of poor fit, but is instead an artifact of visualizing this in log space.

Method 3. monte carlo integration of the expectation

Method 2 should be completely sufficient, but just for fun since we have that integral, it’ll be interesting to numerically approximate the integral itself. This approach won’t give us confidence bounds like method 2 did (unless we calculate a separate integral for the confidence bounds) but it will make estimating the expectation for arbitrarily large values of $n$ tractable.

A quick review of monte carlo integration

To perform monte carlo integration, we need three things:

An interval of integration
A function (the integrand) that we can evaluate everywhere in this range
Upper and lower values that exceed the range of the integrand in the interval of integration

We use the interval of integration and the upper and lower bounds to form a box with known area. The integrand slices this box into two peices. A uniformly random point in this box will lie either above or below the integrand (or, technically, directly on the integrand with probability = 0). By repeatedly generating random points, we can estimate the fraction of the bounding box that is under the integrand. Multiplying the area of the box by this fraction gives us the monte carlo estimate for the area under the curve.

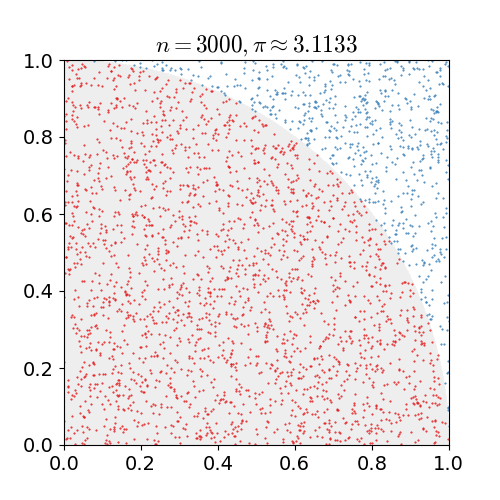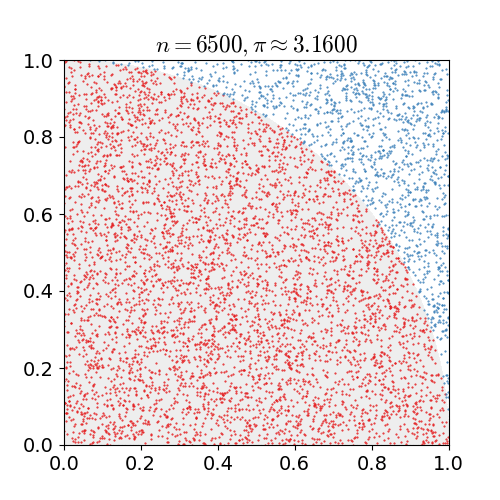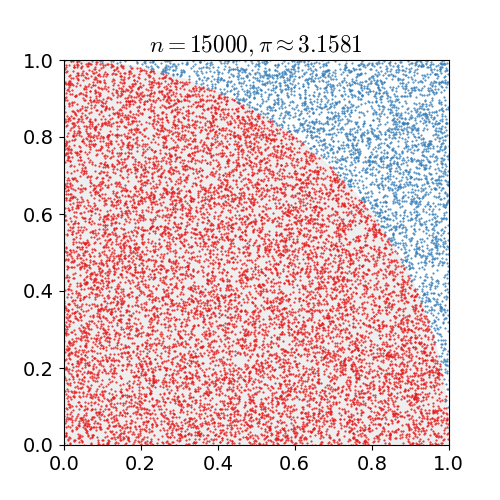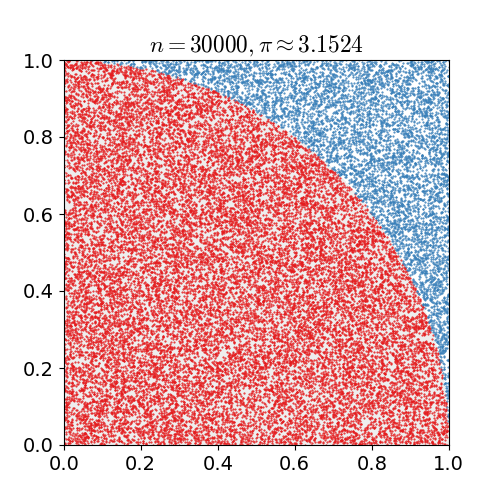
Monte Carlo Integration

mc_int = function(fx, xrange=c(0,1), ymin = 0, ymax=NA, iters=1e6, trace=FALSE){
  xmin = min(xrange); xmax = max(xrange)
  if(is.na(ymax)){
    xv = seq(xmin, xmax, length.out=1e4)
    yrange = fx(xv)
    ymax = max(yrange)*1.25
  } 
  Ux = runif(iters, xmin, xmax)
  Uy = runif(iters, ymin, ymax)
  Y  = fx(Ux)
  test =  Uy < Y
  A = (xmax-xmin) * (ymax-ymin)
  outv = list(estimate = mean(test)*A)
  if(trace) outv$trace = cumsum(test)*A/seq_along(test)
  outv
}

Just to make sure this works, here’s a demo for f(x) = 1:

# MC Integration demo using identity function
plot(mc_int(function(x) 1, ymax=4, trace=TRUE, iters=1e3)$trace, type='l')

With this tool built, now we need to translate the expectation integral as a function, and then we can just run it for different values of $n$ .

# x *  n * F(X)^(n-1) * f(x)
exp_integral = function(x, n){
  x * n * pnorm(x)^(n-1) * dnorm(x)
}
 
# 7s for 1e3 and 5e3
system.time(
  test <- sapply(1:1e3, function(n) 
    mc_int(function(x) exp_integral(x,n), xrange=c(-5,5), iters=5e3)$estimate
    )
)
 
plot(test, type='l')
plot(log(seq_along(test)), test, type='l')

Now, why even go to the trouble? We’ve already got an estimation for this expectation, with confidence bands even, right? Well, although I don’t get confidence bands out of this method, notice how much faster it was.

Monte carlo integration for the confidence intervals

We can use the same technique to get confidence bands.

Sanity checking

With the above estimate for $m ∣ i$ , we can (as earlier) plug it back into our $\frac{1}{1 - F ( x )}$ estimator to estimate $j ∣ i$ .

j_est2 = 1/(1-pnorm(test))
plot(seq_along(j_est2),j_est2, type='l',
     xlab="i", 
     ylab='E[j|i]')

Because I like sanity checks, let’s compare the output of the monte carlo integration with the result from the confidence interval simulation to make sure the new results jive with what we’ve previously seen.

plot(log(seq_along(j_est2)), log(j_est2), type='l',
     xlab="log(i)", 
     ylab='log(E[j|i])')
lines(log(xv), log_j_est[1,], lty=2, col='red')
lines(log(xv), log_j_est[2,], lty=2, col='blue')
lines(log(xv), log_j_est[3,], lty=2, col='red')

Looking good! Now, to demonstrate how powerful the monte carlo integration is, let’s generate estimates for some really large values of $i$ (i.e. large sample sizes). Doing this via simulation would take prohibitively long, but with the monte carlo integration it’s much faster and is really just contingent on how accurate we want to be.

When we ran the monte carlo integration earlier it looked like we started to lose accuracy for large values of $n$ , so I’m going to signficantly boost the number of iterations used for a single numerical integration, which won’t really affect the result much because we’re only going to run this for a limited number of values anyway.

xv = 10^(1:10)
system.time(
  test2 <- sapply(xv, function(n) 
    mc_int(function(x) exp_integral(x,n), xrange=c(-20,20), iters=1e6)$estimate
    )
)
plot(xv, test2, log="x")

And just like that, in basically no time at all, we have fairly high precision estimates of $E [X_{(} n)]$ for arbitrarily large values of $n$ , which would have taken intractably long to calculate using the methods described earlier.

Keep it analytical

I had fun coding up these simulations and stuff, but having pieced together bits and pieces of an analytical solution along the way, it looks like we didn’t really need to go to all that trouble.

Putting it all together

From earlier, we have that the max of an i.i.d. sample of size $n$ with $C D F = F (x)$ is $F (x)^{n}$ . We jumped through a lot of hoops to calculate $E [F (x)^{n}]$ , but it’s pretty much trivial to calculate the median of this statistic, or any quantile. If we plug the result back into the CDF, we get the probability of observing this quantity given the generating distribution. If we plug the resulting probability into the expected value of the geometric distribution, $\frac{1}{p}$ , we get the expected time until we see an observation of at least this magnitude.

$X_{(n)} \sim \frac{d}{d x} F_{X} (x)^{n} s.t. F_{X_{(n)}} = F_{X} (x)^{n}$

$E [X_{(n)}] \approx F_{X_{(n)}}^{- 1} (.5)$

$p_{n} = F_{X} (F_{X_{(n)}}^{- 1} (.5))$

$T_{n} = \frac{1}{p _{n}} = \frac{1}{F _{X} ( F _{X_{(n)}}^{- 1} ( .5 ) )}$

This statistic $T_{n}$ gives us an approximation to the expected number of observations until we see a new max value, given the number of observations we’ve already observed.

xv = seq(-4,4, length.out=1e5)
test = pnorm(xv)^20
 
N=1:20
q=c(.025, .5, .975)
test = sapply(N, function(n) pnorm(xv)^n)
CI_true = apply(test, 2, function(x) sapply(q, function(qi) xv[which.min(qi>x)]))
plot(0, 0, type='n', xlim=c(min(N), max(N)), ylim=c(min(CI_true), ylim=max(CI_true)))
lines(N, CI_true[1,], col='red', lty=2)
lines(N, CI_true[2,])
lines(N, CI_true[3,], col='red', lty=2)

CI2 = 1/(1-pnorm(CI_true))
plot(0, 0, type='n', 
     xlim=c(min(N), max(N)), 
     ylim=c( min(CI2), max(CI2) )
     )
 
lines(N, CI2[1,], col='red', lty=2)
lines(N, CI2[2,])
lines(N, CI2[3,], col='red', lty=2)

Looks familar, right? Let’s overlay this on top of the simulation.

 
plot(0, 0, type='n', 
     xlim=c(min(N), max(N)), 
     ylim=c( min(CI_true), max(CI_true) )
     )
 
lines(N, CI_true[1,], col='red', lty=2)
lines(N, CI_true[2,])
lines(N, CI_true[3,], col='red', lty=2)
 
lines(N, CI[2,N], col='blue', lty=2)
lines(N, CI[1,N], col='blue', lty=2)
lines(N, CI[3,N], col='blue', lty=2)

Oh baby.

Simulating the distribution of wait times

sim_wait_to_new_max_give_sample_size = function(n,
                                                fx=rnorm,
                                                iters=1e3,
                                                q=c(0.025, .5, .975),
                                                values=FALSE){
  outv=list()
  outv$estimate = matrix(NA_real_, length(n), length(q)+1) #rep(NA_real_, length(n))
  if(values) outv$mat = matrix(NA_real_, length(n), iters)
  for(i in 1:length(n)){
    sim_i = rep(NA_real_, iters)
    for(j in 1:iters){
      x = fx(n[i])
      m0 = max(x)
      m1=m0-1
      k=0
      while(m0>m1){
        k=k+1
        m1=fx(1)
      }
      sim_i[j] = k
    }
    if(values) outv$mat[i,] = sim_i
    outv$estimate[i,] = c(mean(sim_i), quantile(sim_i, q))
  }
  outv
}

xv=1:20
system.time(test <- sim_wait_to_new_max_give_sample_size(xv, iters=5e3, values=TRUE))
#plot(xv, test$estimate, type='l')
plot(0, 0, type='n', 
     xlim=c(min(xv), max(xv)), 
     ylim=c( min(test$estimate), max(test$estimate[,4]) )
)
lines(xv, test$estimate[,1], col='blue')
lines(xv, test$estimate[,3], lty=2)
lines(xv, test$estimate[,2], col='red', lty=2)
lines(xv, test$estimate[,4], col='red', lty=2)
 
lines(N, 1/(1-pnorm(CI_true[1,])), col='red')
lines(N, 1/(1-pnorm(CI_true[2,])))
lines(N, 1/(1-pnorm(CI_true[3,])), col='red')

The secretary problem

…

David Marx

Explorer

A Statistical Argument For Settling: a foray into extreme value theory